複利は、投資や貯蓄において非常に重要な概念であり、資産を増やすための強力な手段です。本ドキュメントでは、複利の基本的な仕組み、計算方法、そしてその効果について詳しく解説します。
複利とは?
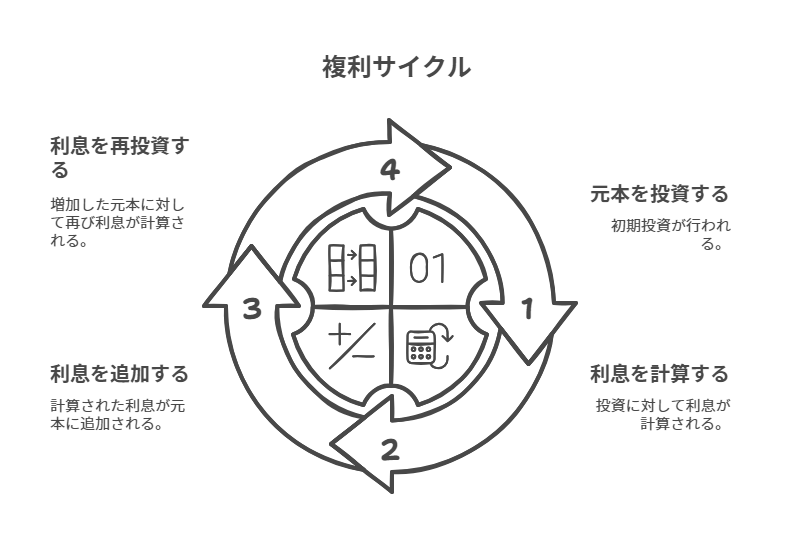
複利とは、元本に対して利息が計算され、その利息が次の期間の元本に加算される仕組みを指します。これにより、利息が利息を生むことになり、時間が経つにつれて資産が加速度的に増加することが可能になります。
お金を借りるときも、この利息が適用されますので、少ししか借りていないつもりでも返す金額はバカ高くなるのは同じ理屈です。
🆚 単利との違い
| 種類 | 説明 | 利息がつく対象 |
|---|---|---|
| 単利 | 毎回、元本に対してのみ利息がつく | 元本のみ |
| 複利 | 毎回、元本+それまでの利息に対して利息がつく | 元本+利息 |
複利の計算方法
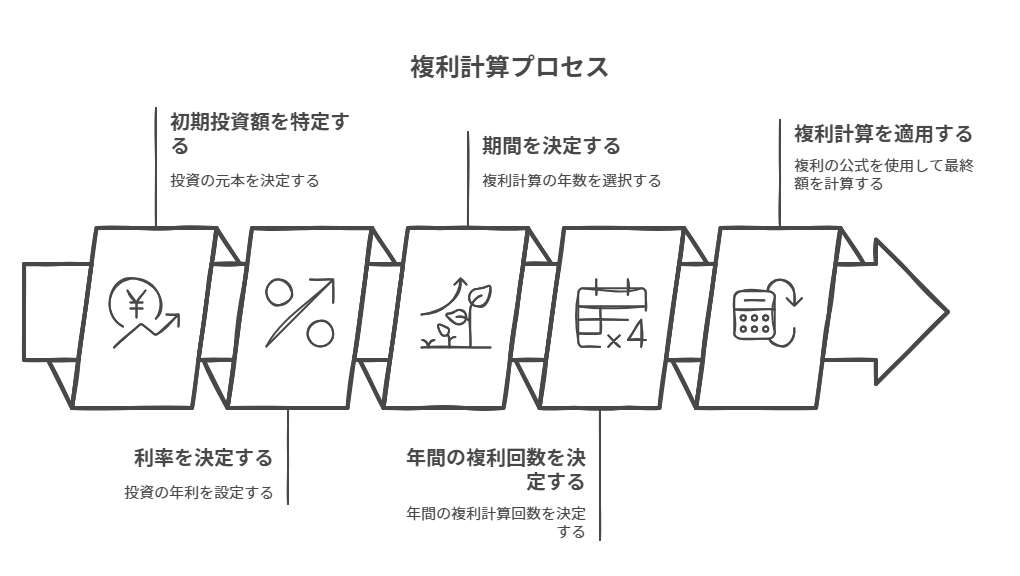
複利の計算式は以下のようになります。
\[A = P(1 + r/n)^{nt}\]
ここで、
\(A\) は将来の総額(元本 + 利息)
\(P\) は元本
\(r\) は年利率(小数で表す)
\(n\) は利息が計算される頻度(年に何回か)
\(t\) は投資期間(年数)
例
例えば、元本が100万円、年利率が5%、利息が年に1回計算される場合、5年後の総額は次のように計算されます。
\(P\) = 1,000,000
\(r\) = 0.05
\(n\) = 1
\(t\) = 5
\[A = 1,000,000(1 + 0.05/1)^{1 \times 5}\]
\[A = 1,000,000(1.05)^{5}\]
\[A \approx 1,276,281\]
この場合、5年後の総額は約127万6281円になります。
複利の効果
複利の効果は、時間が経つにつれて顕著になります。長期間にわたって投資を続けることで、資産は指数関数的に増加します。例えば、同じ年利率であっても、投資期間が長いほど、最終的な資産額は大きくなります。
重要なポイント
| 年数 | 金額(円) |
| 1年後 | 1,050,000 |
| 5年後 | 1,276,282 |
| 10年後 | 1,628,895 |
| 20年後 | 2,653,298 |
| 30年後 | 4,321,942 |
早期の投資: 複利の効果を最大限に活かすためには、早期に投資を始めることが重要です。
再投資: 利息を再投資することで、さらに資産を増やすことができます。
長期的視点: 短期的な利益を追求するのではなく、長期的な視点で資産形成を考えることが大切です。
複利のポイント
- 長期運用がカギ:期間が長いほど効果が大きくなる
- 利率の影響大:わずかな利率の差が、長期では大きな差に
- 再投資が大事:利息を使わずに再投資し続けること
複利のしくみ、まとめ
複利は、資産を増やすための強力なツールです。元本に対して利息が計算され、その利息が次の元本に加算されることで、時間が経つにつれて資産が増加します。早期に投資を始め、利息を再投資することで、複利の効果を最大限に活かすことができます。長期的な視点で資産形成を考えることが、成功への鍵となります。